The osculating circle on a curve for a specific parameter

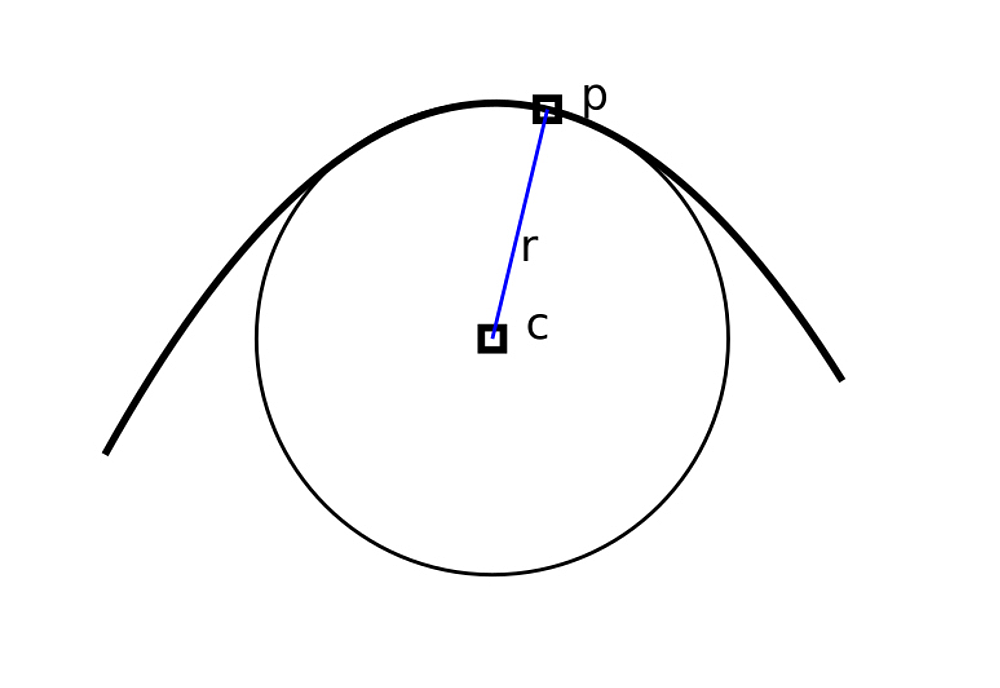
Fig: Curve with osculating circle

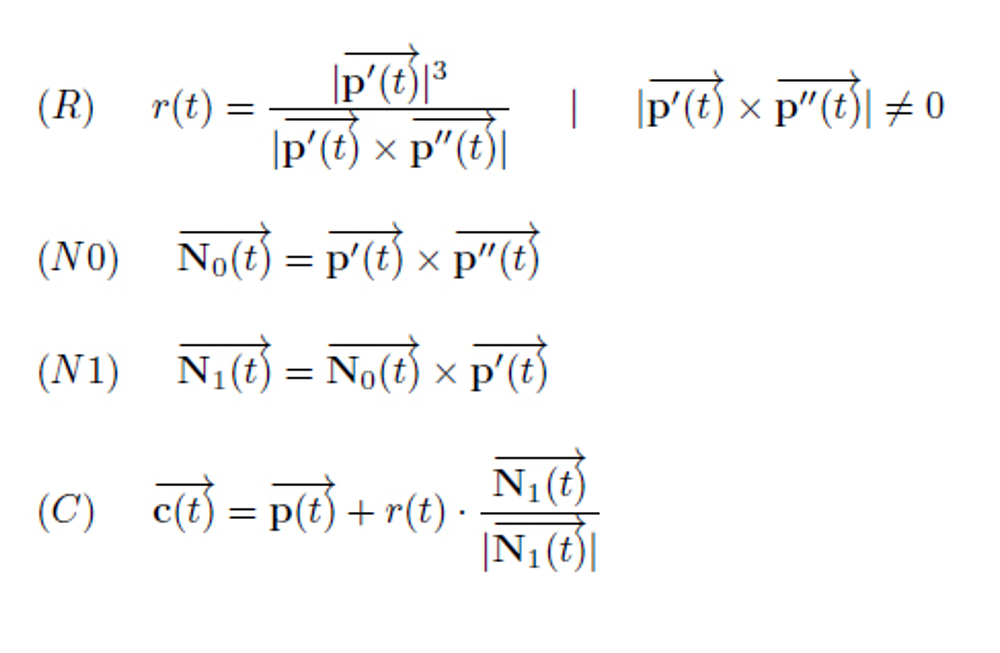
Fig: The formulas for the osculating circle

These formulas are no longer as trivial as those for the derivatives.

The formulas move freely in 3d space (the cross product is always used), but they are also valid for 2d curves.

Concerning formula (R): r(t) is not defined if either

• the first or second derivative in t does not exist, or

• the first or second derivative is equal to the zero vector, or

• the first and second derivatives have the same direction (or the exact opposite direction).

In all these cases, the denominator of the fraction is zero and r(t) is not defined and there is no meaningful osculating circle.

(N0) calculates a vector that is perpendicular to p'(t) and p''(t). I.e, N0(t) defines a plane in which both p'(t) as well as p''(t) are located.

(N1) then results in a vector lying in the plane defined by (N0) and is perpendicular to p'(t) .

(C) finally calculates the center of the osculating circle.

Unfortunately, there is no particular specialization of these formulas for the Svg objects. At most, you can consider whether the vector N0(t) is constant independently of t, so that it only needs to be calculated once.