Der Schmiegekreis an eine Kurve für einen bestimmten Parameter
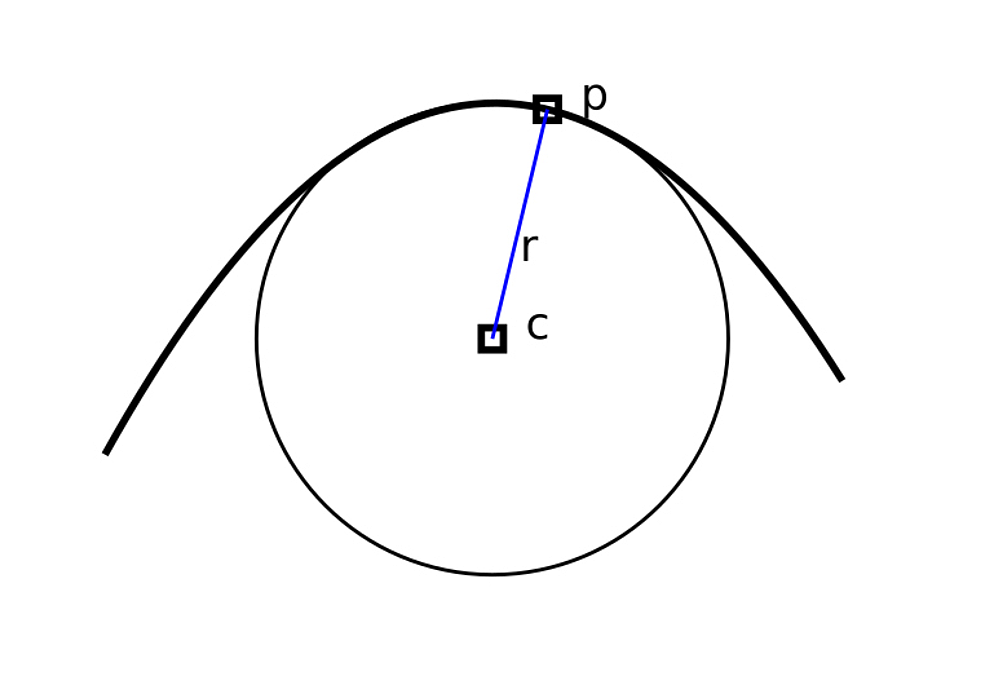
Abb.: Kurve mit Schmiegekreis
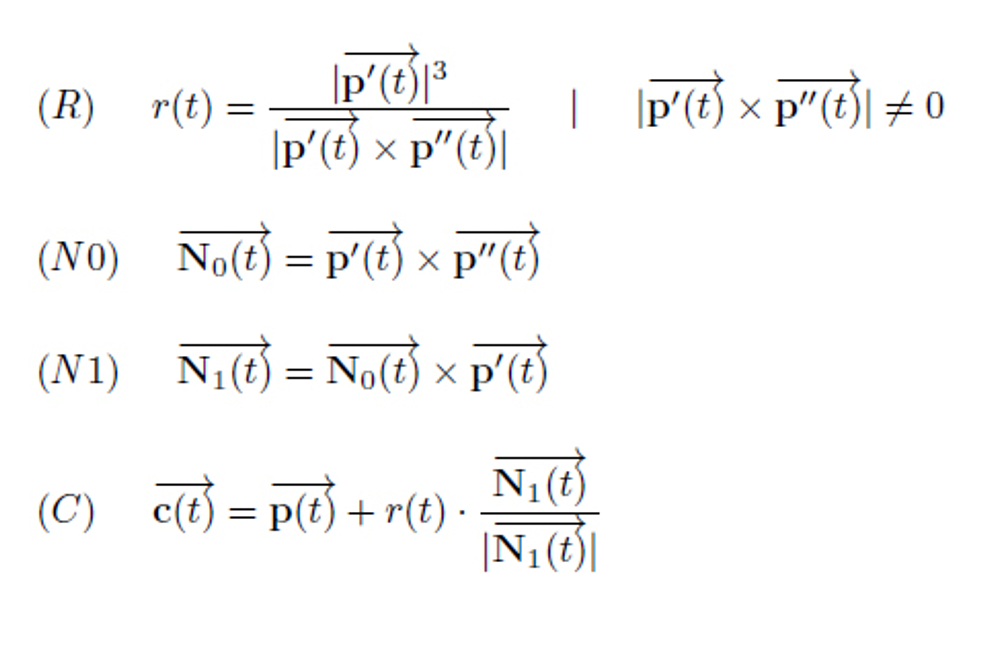
Abb.: Die Formeln für den Schmiegekreis
Diese Formeln sind schon nicht mehr so trivial wie die für die Ableitungen.
Die Formeln bewegen sich munter im 3d-Raum (es wird ja ständig das Kreuz-Produkt verwendet), sie sind aber auch für 2d-Kurven gültig.
Zur Formel (R): r(t) ist dann nicht definiert, wenn entweder
die erste bzw. zweite Ableitung in t nicht existiert, oder
die erste bzw. zweite Ableitung gleich dem Nullvektor ist, oder
die erste und die zweite Ableitung die gleiche Richtung haben (oder die genaue Gegenrichtung).
In all diesen Fällen ist der Nenner des Bruches nämlich Null und r(t) nicht definiert und es gibt keinen sinnvollen Schmiegekreis.
(N0) errechnet einen Vektor, der auf p'(t) und p''(t) senkrecht steht. D.h., N0(t) definiert eine Ebene, in der sowohl p'(t) als auch p''(t) liegen.
(N1) ergibt dann einen Vektor, der in der Ebene liegt, die von (N0) definiert wird, und senkrecht auf p'(t) steht.
(C) schließlich errechnet den gesuchten Mittelpunkt des Schmiegekreises.
Leider gibt es keine besondere Spezialisierung dieser Formeln für die Svg-Objekte. Man kann sich höchstens überlegen, ob vielleicht der Vektor N0(t) unabhängig von t konstant ist, so dass man ihn nur einmal berechnen muss.