Die Ableitungen einer Vektor-wertigen Kurve in 3d

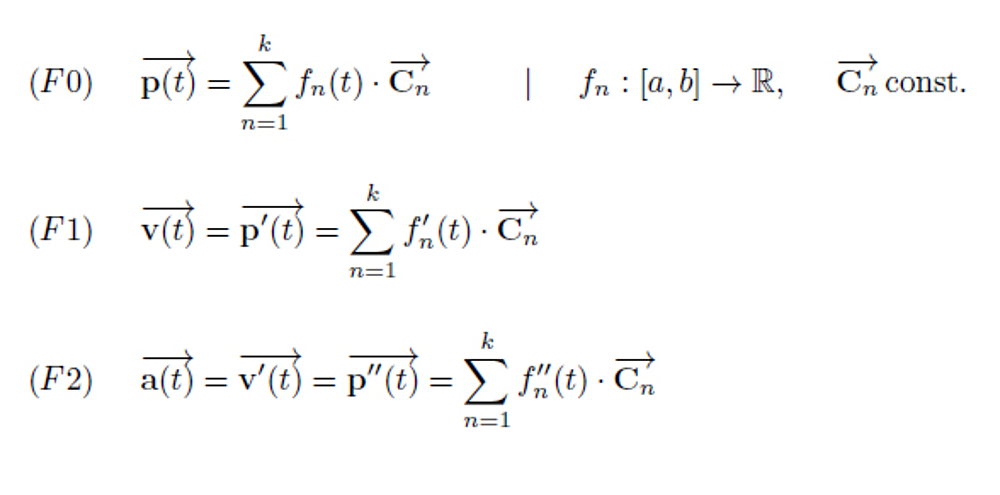
Abb.: Die Formeln für den Ortsvektor, die Tangente und die 2. Ableitung

Die 3 Formeln sind eigentlich trivial.

Die Formel (F0) beschreibt den Ortsvektor p in Abhängigkeit vom Parameter t. Dabei sollen die Vektoren Cn konstant sein. Ändern tun sich hier nur die Werte der Funktionen fn(t). So eine Darstellung ist ja immer zu finden. Allerdings sollte die Anzahl der Summanden dabei möglichst klein sein, damit der Rechenaufwand gering bleibt. Die Vektoren Cn müssen dann für jede Kurve nur einmal berechnet werden.

Die Formeln (F1) und (F2) für die erste und zweite Ableitung ergeben sich dann ganz zwangsläufig aus (F0). Weil die Vektoren Cn ja konstant sind, müssen nur die Funktionen fn(t) abgeleitet werden. Die Existenz dieser Ableitungen wollen wir hier voraussetzen (wenigstens für den Parameter t)

(F1) beschreibt dann die Geschwindigkeit bzw. die Tangente. Die Richtung der Geschwindigkeit ist von der jeweilen Parametrierung unabhängig. Allerdings hängt der Betrag der Geschwindigkeit schon von der Parametrierung ab.

(F2) beschreibt analog dazu die Beschleunigung bzw. die Krümmung.