The derivatives of a vector-valued curve in 3d

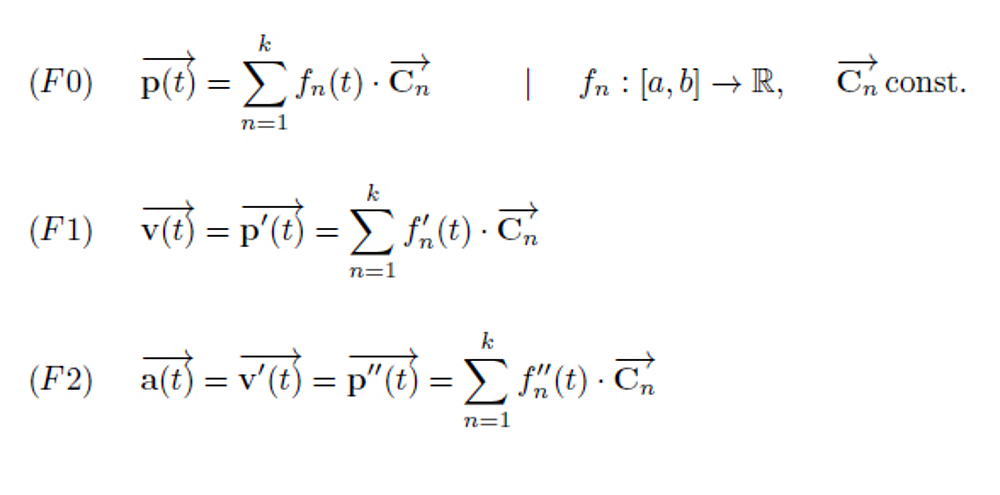
Fig: The formulas for the position vector, the tangent line and the 2. Derivation

The 3 formulas are actually trivial.

The formula (F0) describes the position vector p as a function of the parameter t. The vectors Cn shall be constant. Only the values of the functions fn(t) change here. You can always find such a representation. However, the number of summands should be as small as possible so that the calculation effort remains low. The vectors Cn then only need to be calculated once for each curve.

The formulas (F1) and (F2) for the first and second derivatives are then inevitably derived from (F0). Because the vectors Cn are constant, only the functions fn(t) must be derived. We are assuming the existence of these derivatives here (at least for the parameter t)

(F1) then describes the speed or the tangent. The direction of the speed is independent of the respective parameterization. However, the amount of speed already depends on the parameterization.

(F2) describes the acceleration or curvature in the same way.