The formulas for the cubic Bezier curve

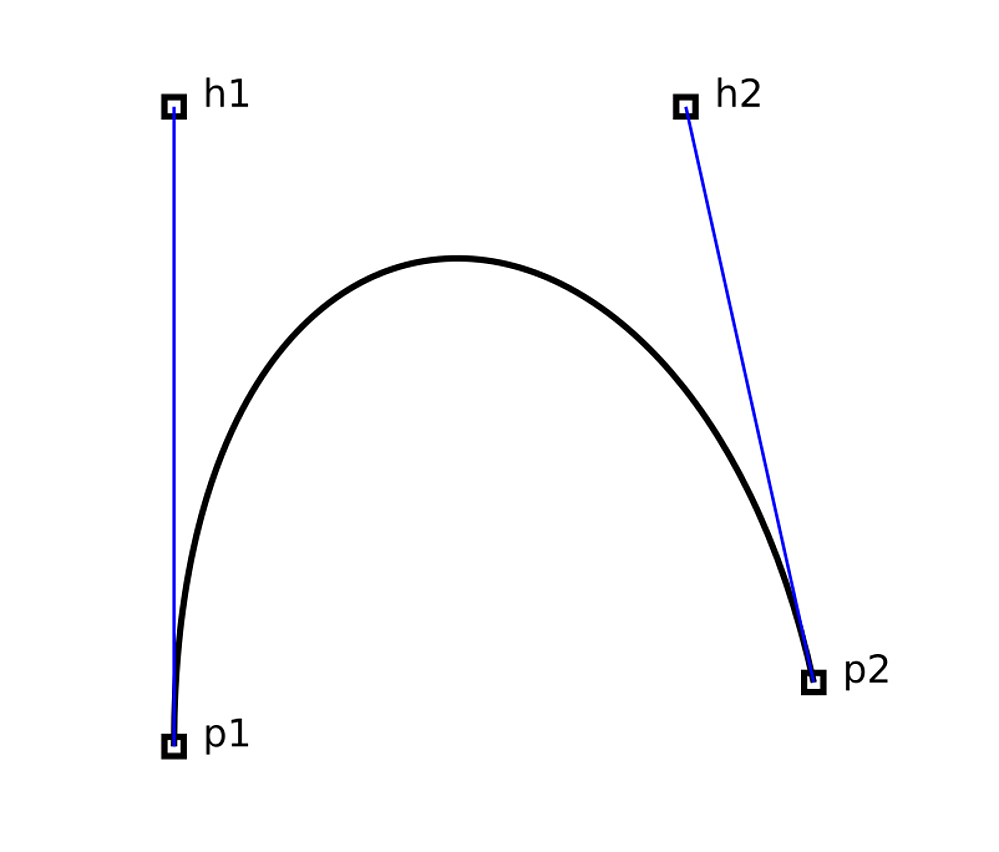
Fig: An example of a cubic Bezier curve

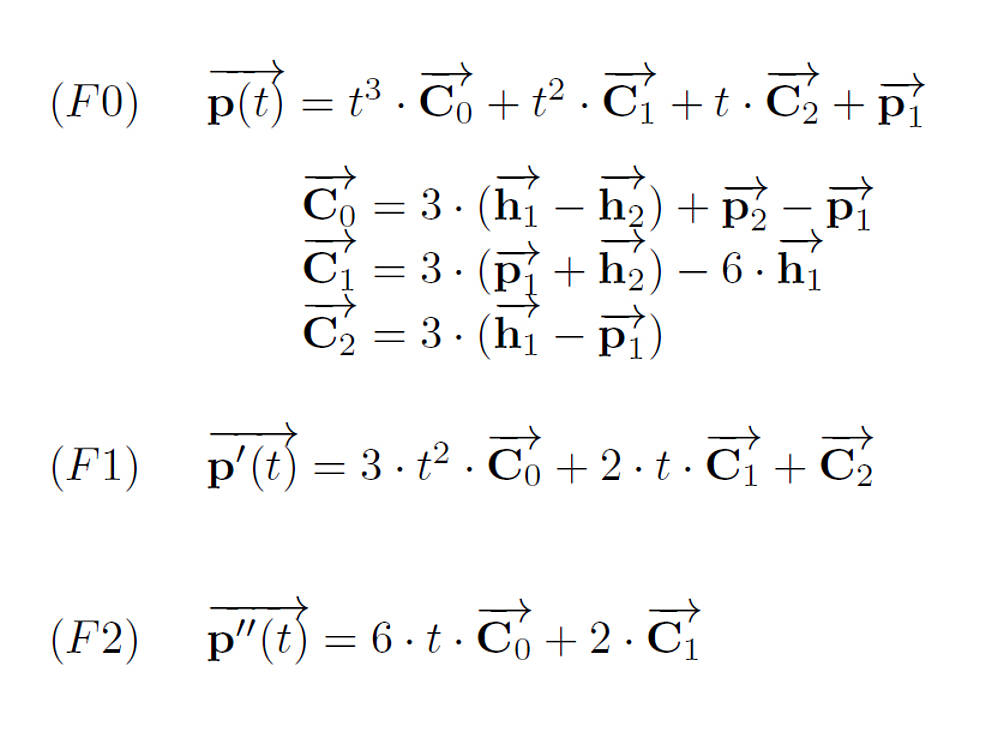
Fig: The curve formulas for the cubic Bezier curve

If you want to reconstruct these formulas yourself, I recommend using the algorithm by de Casteljau.

This curve is determined by four points. It would therefore be possible to create a curve that no longer fits in exactly one plane by selecting suitable points. With the normal definition by Svg paths, this is of course irrelevant.

As for the osculating circle: there are lots of strange shapes with kinks, loops and straight sections in cubic curves. So far, I don't know of any algorithm that accurately predicts the route from the 4 given points. I would therefore recommend using the vector N0 from the osculating formula always for the respective parameter t is calculated.

If you have any information on how to recognize any special features from the points, I would be very grateful for a link.