Die Formeln für die kubische Bezier-Kurve

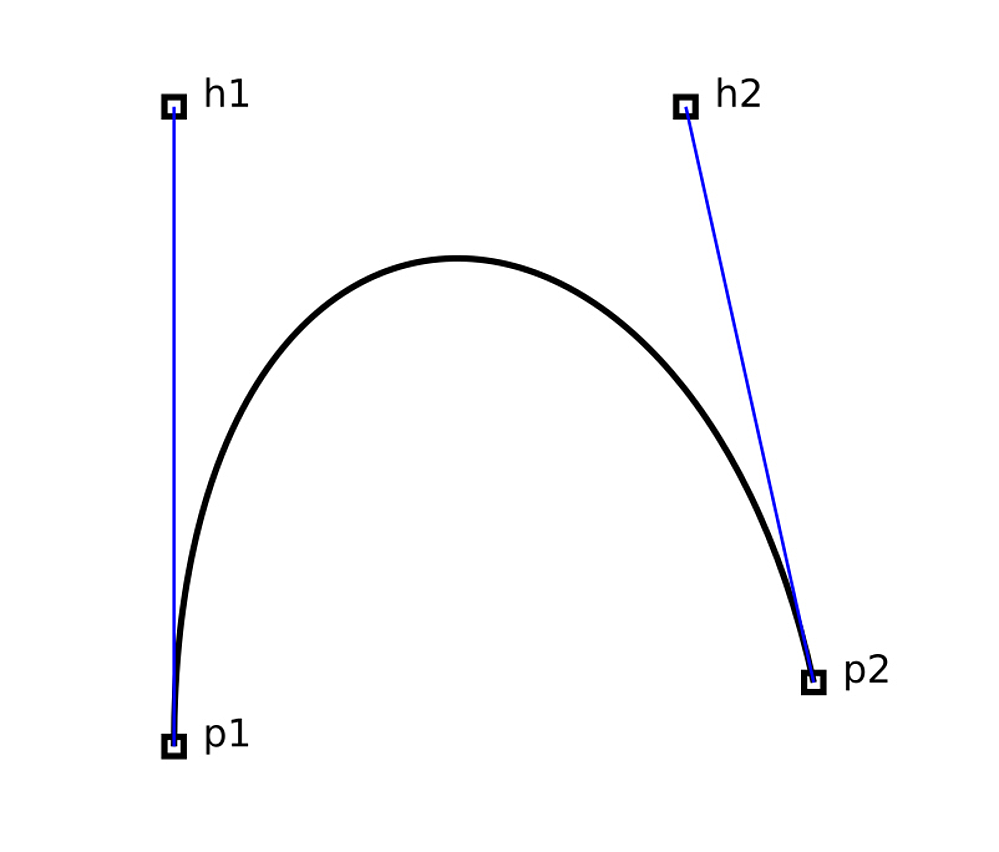
Abb.: Ein Beispiel für eine kubische Bezier-Kurve

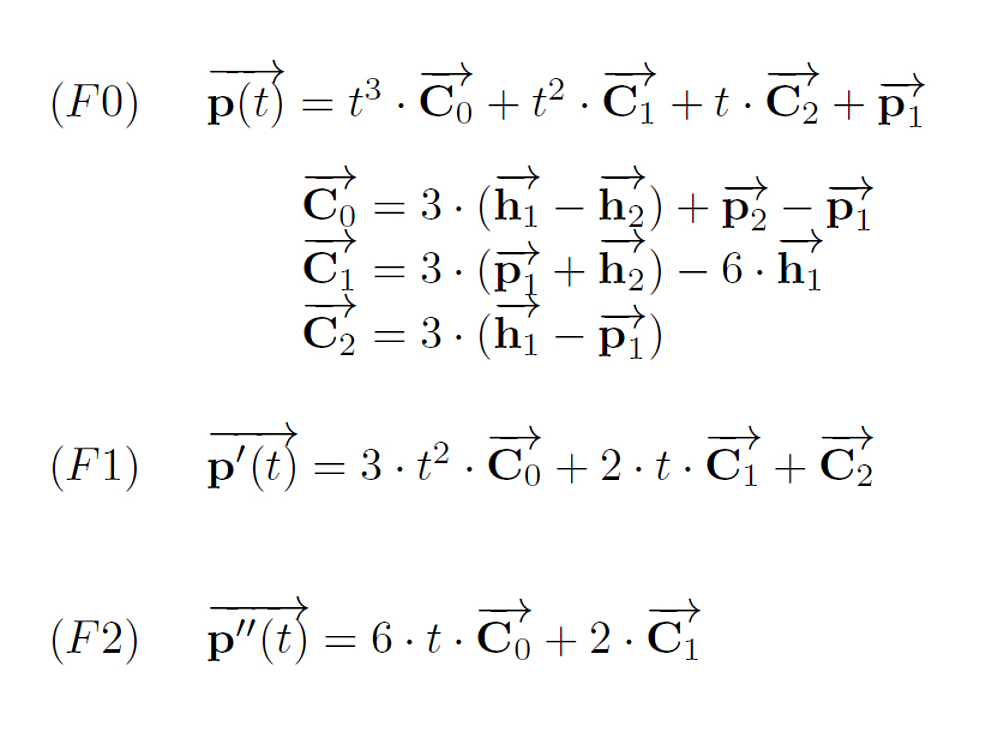
Abb.: Die Kurven-Formeln für die kubische Bezier-Kurve

Falls Sie die Herleitung dieser Formeln selbst nachvollziehen wollen, empfehle ich den Algorithmus von de Casteljau.

Diese Kurve wird von vier Punkten bestimmt. Es wäre also möglich, durch eine geeignete Wahl der Punkte eine Kurve zu erzeugen, die nicht mehr in genau eine Ebene passt. Bei der normalen Definition durch Svg-Pfade ist das natürlich irrelevant.

Was den Schmiegekreis angeht: es gibt bei den kubischen Kurven jede Menge seltsame Formen mit Knicken, Schleifen und geraden Abschnitten. Ich kenne bis jetzt keinen Algorithmus, der aus den 4 gegebenen Punkten sauber den Verlauf voraussagt. Ich würde also empfehlen, den Vektor N0 aus der Schmiege-Formel immer für den jeweiligen Parameter t auszurechnen.

Falls Sie Information darüber haben, wie man aus den Punkten irgendwelche Besonderheiten erkennen kann, wäre ich für einen Link sehr dankbar.