Die Formeln für den Svg-Ellipsenbogen

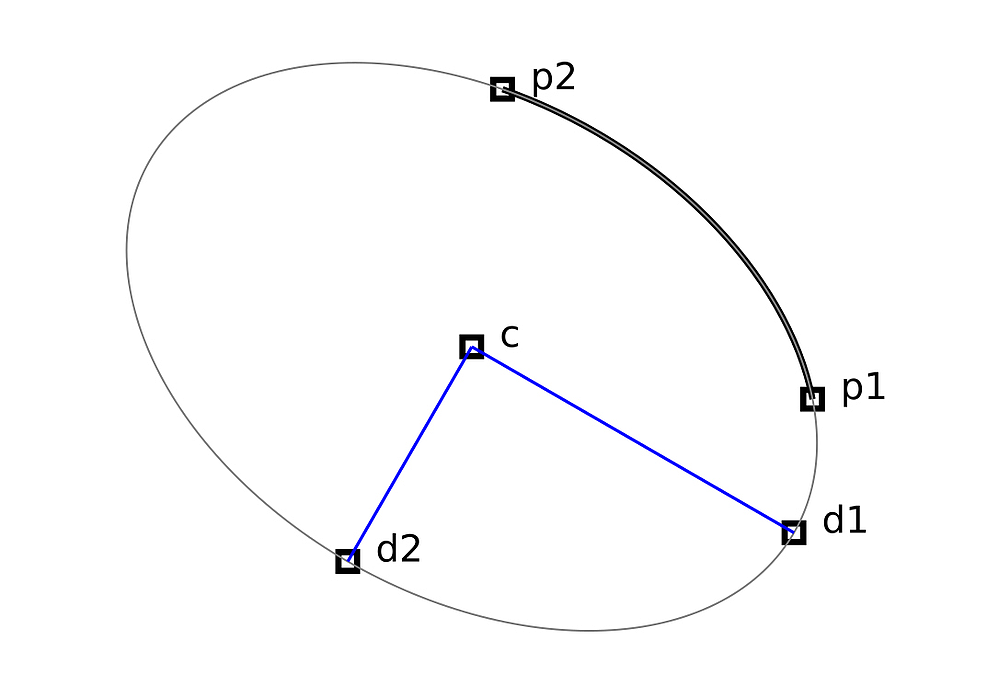
Abb.: Ein Svg-Ellipsen-Bogen

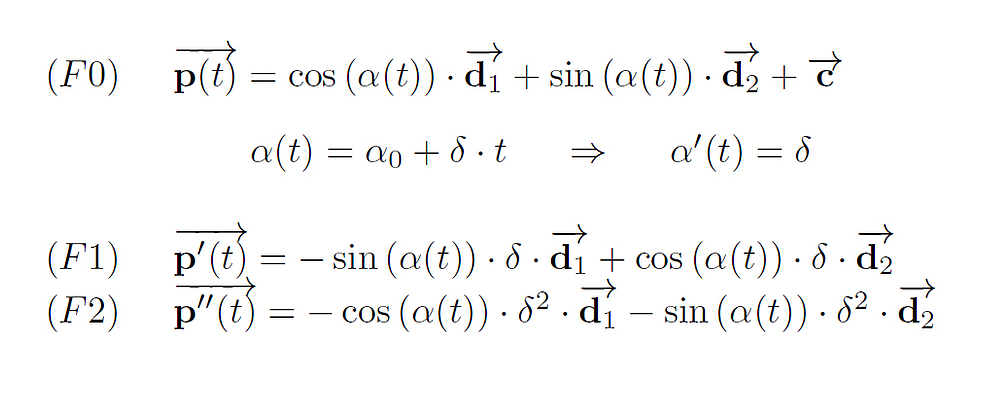
Abb.: Die Kurven-Gleichungen für elliptische Svg-Bögen

Es ist erstaunlich, wie kompliziert das Berechnen der Ellipsen- (und Kreis-)Bögen ist, verglichen mit den Bezierkurven. Die erste Herausforderung ist schon die Berechnung des Mittelpunkts c. Die Pfadbeschreibung für den Bogen funktioniert nämlich ohne die Angabe des Zentrums. Dafür ist sichergestellt, dass Anfangs- und Endpunkt genau eingehalten werden. Diese Berechnung soll hier nicht dargestellt werden, s. z.B. die Beschreibung bei w3.org. Wenn man das Zentrum hat, ist die Berechnung der beiden Hauptachsenvektoren d1 und d2 nicht mehr schwer.

Bitte beachten Sie dass d1 und d2 der jeweilige Differenz-Vektor vom Mittelpunkt c aus ist.

Die Funktion alpha(t) kommt aus dem Wunsch, den Parameterbereich von 0 bis 1 zu verwenden. alpha0 ist dabei der Winkel des Startpunktes p1 des Bogens, und delta is die Größe des Winkels vom Startpunkt zum Endpunkt p2 (die Winkel sind bezogen auf die beiden Hauptachsen).

Diese Kurve wird durch 3 Vektoren bestimmt. Also liegt sie grundsätzlich in einer Ebene. Auch die Orientierung bleibt gleich und der Vektor N0 für die Berechnung des Schmiegekreises hängt nicht vom Parameter t ab und muss nur einmal berechnet werden. Hier existiert für jeden Parameterwert t ein Schmiegekreis. Falls die Ellipse einen echten Kreis bezeichnet, ist der Schmiegekreis identisch mit diesem Kreis.

Für die Definition eines Bogens wird ja die Orientierung ("mit oder gegen den Uhrzeigersinn") verwendet. Bitte beachten Sie, dass hier die Orientierung des Koordinatensystems eine Rolle spielt.