The formulas for the Svg elliptical arc

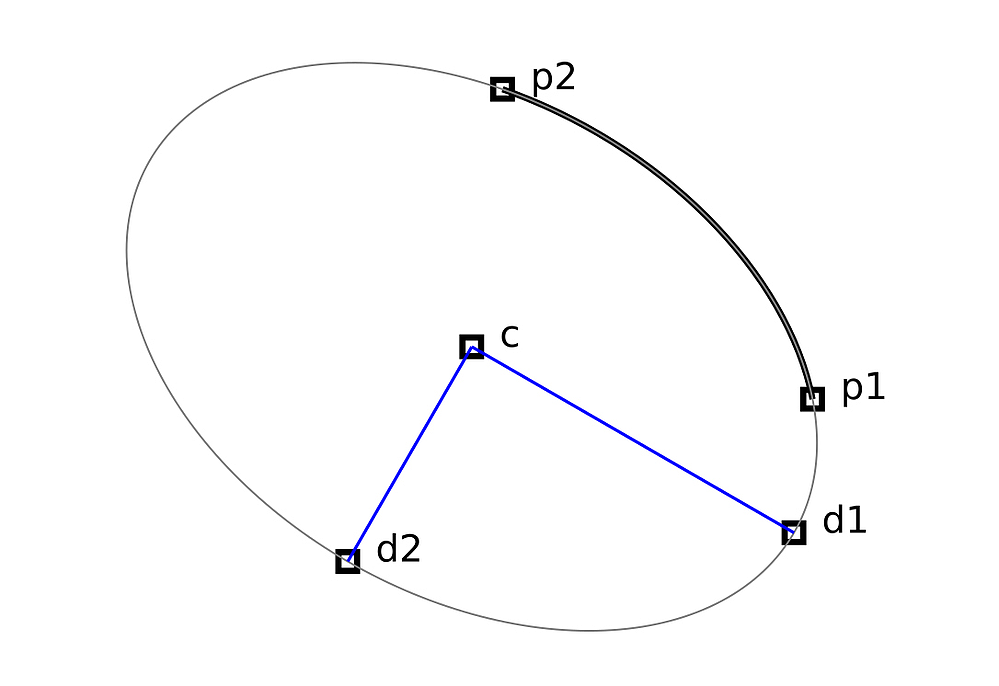
Fig: An Svg elliptical arc

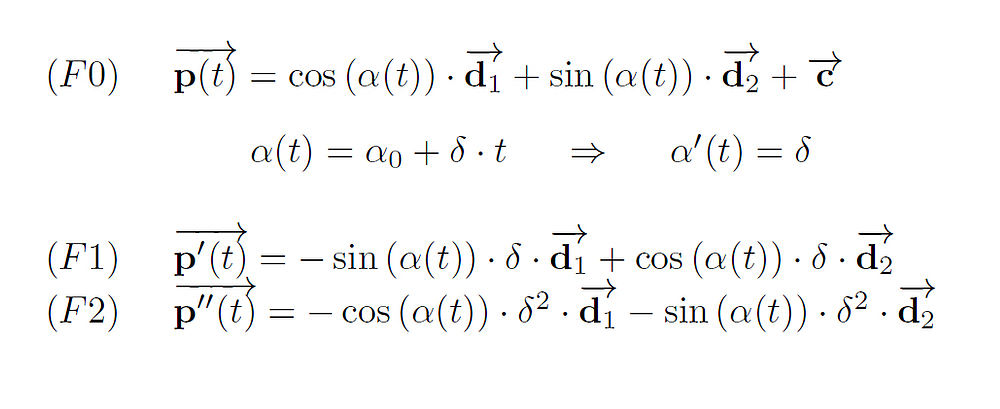
Fig: The curve equations for elliptical Svg arcs

It is amazing how complicated it is to calculate the elliptical (and circular) arcs compared to the Bezier curves. The first challenge is the calculation of the center point c. The path description for the arc works without specifying the center. This ensures that the start and end points are precisely adhered to. This calculation will not be shown here, see e.g. the description at w3.org. If you have the center, the calculation of the two main axis vectors d1 and d2 is no longer difficult.

Please note that d1 and d2 are the respective difference vector from the center c.

The function alpha(t) results from the desire to use the parameter range from 0 to 1. alpha0 is the angle of the starting point p1 of the arc, and delta is the size of the angle from the starting point to the end point p2 (the angles are related to the two main axes).

This curve is determined by 3 vectors. So it is basically in one plane. The orientation also remains the same and the vector N0 for calculating the osculating circle does not depend on the parameter t and only needs to be calculated once. Here, for each parameter value t there is an osculating circle. If the ellipse denotes a true circle, the osculating circle is identical to this circle.

The orientation ("clockwise or counterclockwise") is used to define an arc. Please note that the orientation of the coordinate system plays a role here.